Fun and Games: Explore the Power of Game Theory

Introduction

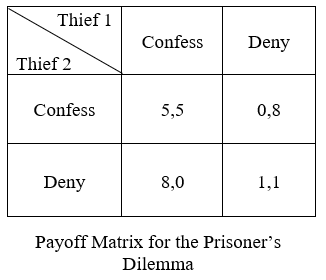
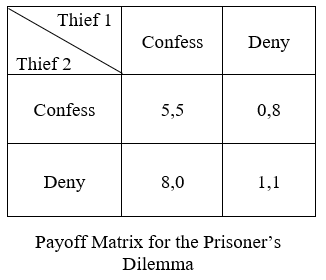
You and your partner have just committed the heist of the century. For a while you were on top of the world, but now it’s time to face the consequences. The police have taken both of you to be interrogated separately, and you have no means of communicating with your partner. As you wait in the holding cell, you manage to hear a snippet of the conversation outside and realize the police actually don’t have evidence to convict you of the heist - so they are going to offer you and your accomplice two options: confess or deny. If both of you confess, they will sentence you to 5 years in jail. If on the other hand, you confess but your partner denies, you will go scot-free and your partner will receive 8 years in jail. However the same holds true if you deny and your partner confesses. And finally, if you both deny then the police only have evidence to convict you on a minor charge and will sentence you to 1 year in prison. You only have a couple of minutes before they come to your cell, so you need to decide fast. What do you do?

This is the classic example of game theory known as the Prisoner’s Dilemma, recognized for its surprising result. While it may seem that the rational choice is to deny, as it works out to be a shorter sentence for both of you, when we work through the details it turns out to be the opposite. Let’s assume your partner confesses. Then you are better off confessing rather than denying (5 as opposed to 8). What about if your partner denies? Then confessing is still the better option (0 as opposed to 1)! As you run through the cases, you realize that your partner has also come to the same conclusion, and so you start preparing yourself for the next 5 years in prison.

Background

This surprising result arises from the seemingly simple concept of a decision. We make thousands of them every day – some large, life-changing ones, and others that we barely notice at all. Each decision, whether it’s navigating international politics, making compromises, or negotiating the price of a mango, is a complex process of assessing different risks and trying to maximize your gains. There are a variety of factors to consider – so much so that trying to break down the process will quickly become a logistical nightmare. That’s where game theory comes in. Game theory is the study of the interactions between perfectly rational “players” based on certain rules – like the Prisoner’s Dilemma. Using mathematics, game theory serves to analyze such “games” to gain a deeper understanding of even the most complex scenarios. While it may seem that its use is limited to contrived examples or simple children’s games, game theory has applications that spread far and wide, and it pertains to every decision that you make.

Before learning about why game theory is so ubiquitous, it’s important to understand the basic terminology and foundations of the subject in order to truly appreciate its beauty. First of all, we have to define what a game is as well as some related terms. Put simply, “a game is the set of rules that describe it. An instance of the game from beginning to end is known as a play of the game. And a pure strategy… is an overall plan specifying moves to be taken in all eventualities that can arise in a play of the game” (Royce). Although these definitions are vague and allow for a variety of different games, we can usually categorize them according to some simple attributes. For example, a perfect information game is one where all the players know all the rules, possible choices, and past moves of the game - like chess - and an imperfect one is where some information is hidden - like poker. Additionally we have 2-player games, 3-player games, or more generally n-player games (if it can be played by multiple “players”). One more important definition is a zero-sum game where the expected reward of winning/losing a game, when played multiple times, is zero.

Game theory is designed to take apart these games and come up with a rational strategy in order to win - or at least to beat everyone else. In the early-to-mid 20th century the subject was revolutionized by multiple mathematicians, particularly John von Neumann and John Nash. Both of them worked on a surprising result on an equilibrium strategy for all players such that there is no incentive or gain from deviating, which is called a Nash equilibrium. In other words, this strategy is the best response to itself, much like the choice of confessing in the Prisoner’s Dilemma. Not only that, but they found that there can exist multiple of these equilibria so there can be more than one rational strategy! In fact, one of the most important theorems in game theory, the Nash Equilibrium Existence Theorem, dictates that any game with a finite amount of players with finitely many strategies has at least one Nash Equilibrium - a result that was proved by Nash himself. This very mathematical, theoretical, and seemingly useless theorem actually won Nash a Nobel Prize… in economics!

Economics

It might seem odd that the Nobel Committee would hand out an award for something as trivial as a game; however, because of our loose definition of a game, it’s possible to represent real-world and extremely applicable scenarios in terms of sets of rules with causes and effects. For example, consider a duopoly where two firms are the main manufacturer of a product and they are trying to decide what price they should charge. This is a very complex situation: setting a cheap price would result in more sales by undercutting the opponent, but perhaps an overall decrease in revenue - and vice versa for a more expensive price. However, we can use game theory to create a model of the situation and apply some math to find the Nash Equilibrium strategy for this “game.” But game theory is not just limited to market analysis - it can also be applied to behavioral economics to predict what people will buy depending on how a product is advertised. In fact, behavioral economics is the study of the psychology of how people make economic decisions; it is natural to use the lens of game theory for analysis. This subject had such a profound influence on economics that some business majors are required to take at least one game theory course during their studies, so “it seems a safe bet that game theory will continue to be the language of economics” (Samuelson 20). However, the economy is extremely versatile and flexible, so it can be hard to take into account factors like international relationships and political motivations. As it turns out, game theory can be used for that as well.

International Politics

Stepping back and taking a broad overview of international politics, it’s easy to see where a game theoretical analysis could be useful. Every individual country is looking out for themselves, but they can’t function without interactions between other nations. Immigration, trade, foreign policy, and tourism are all things that independent states need to consider in order to make a decision that would benefit them. When countries come together for treaties and agreements, we can use models based on n-player games to see what the rational choice is. Take the arms race as an example. Similar to the Prisoner’s Dilemma, everyone would be better off if all nuclear weapons were dismantled and destroyed. However, one country has a lot to gain by being the only country with nukes (it would increase their leverage in many situations). Therefore, the Nash equilibrium is reached when both sides continue to build up their nuclear arsenal - which is what we saw during the Cold War. Many more instances throughout history can be represented through such models. For example, the General Agreement on Tariffs and Trade (GATT) has a game-theoretic reasoning behind its success, as did the Strategic Arms Limitation Talks (SALT), which reduced the tension between the US and Soviet Union during the Cold War. The adaptability and simplicity of models in game theory “has a richness that makes it amenable to such broad empirical application. The theoretical constructs are flexible and can be adapted to different substantive problems” (Snidal 33-34). By analyzing these historical situations, it’s even possible to predict what future relations might look like between different countries - a tool that is extremely valuable in today’s world.

Military and Defense

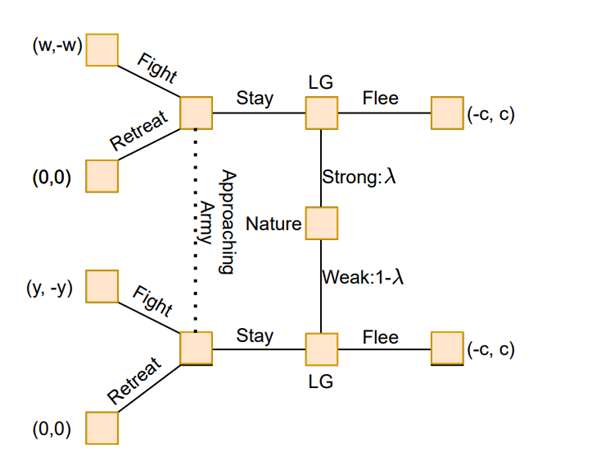
However, sometimes political relationships go awry and war is on the line. How can a country make the best use of its resources and military to most efficiently protect itself and attack its enemy? It turns out that game theory in defense applications actually isn’t a new idea: the Chinese military used some core concepts in order to outsmart their enemies. In one example, a Chinese general named Zhuge Liang had a very small army that was defending a city. As a large and more powerful army approached, Liang had to make a decision - either defend the city and most likely lose or flee and still lose the city. However Liang realized he could take advantage of an imperfect information signaling game. He ordered his army to hide within the city and Liang sat in an unassuming position at the top of his tower and started playing music. As the enemy approached, they were unaware of the size of Liang’s army but from the signal that Liang was sending it seemed as if he was setting up an ambush. As such, the opposing general took the safest option and left the city alone. We can even see examples of game theory in stories of the English Navy. Long story short, there was a particular tactic that served as a Nash Equilibrium for ships in a naval battle called a “line of battle,” such that there is no gain from trying anything else. However, in one English battle against the Franco-Spanish navy, certain circumstances changed the best response to the “line of battle,” which the English took advantage of to win. In a similar vein, game theory can be applied to almost every aspect of defense from aerial warfare to cyber security because it “enhances military strategies and decision making processes with a holistic and quantitative analysis of situations” (Ho et. al. 2). In essence, game theory has the potential to save lives - and in fact, has saved lives, because of the powerful analytical tool that it provides.

Decision Tree for the Empty City Signaling Game (Ho et.al. 13)

Conclusion

Hopefully it is now apparent that game theory is very different from “fun and games.” Instead it is a powerful mathematical tool that can be used to analyze all sorts of situations where people, robots, countries, and even different species interact. Its applications are varied, and there are likely more that we have yet to discover in completely different fields! While its models are relatively simple, it still manages to capture and accurately represent detailed and complex scenarios. For example, selecting which colleges to apply to can be a stressful decision. Thankfully, game theory has got you covered. In fact, some researchers have worked with the education system in their area to create a process that could take into account factors like rate of acceptance, popularity, and student performance! Or consider something as simple as negotiating the price of a notebook. Game theory can help you bargain your way down to the Nash Equilibrium where both you and the seller are happy! Any decision, both big and small, complex and simple, life-changing or dull, can be intricately studied and explored using the power of game theory.

Sources:

Ho, Edwin, et al. “Game Theory in Defence Applications: A Review.” Sensors (Basel, Switzerland), vol. 22, no. 3, 2022, pp. 1032-, https://doi.org/10.3390/s22031032.

Royce, B. “What Is Game Theory and What Are Some of Its Applications?” Scientific American, vol. 289, no. 6, SCI AMERICAN INC, 2003, pp. 124–124.

Samuelson, Larry. “Game Theory in Economics and Beyond.” The Journal of Economic Perspectives, vol. 30, no. 4, 2016, pp. 107–30, https://doi.org/10.1257/jep.30.4.107.

Snidal, Duncan. “The Game Theory of International Politics.” World Politics, vol. 38, no. 1, 1985, pp. 25–57, https://doi.org/10.2307/2010350.