Graph Theory: Connecting the Dots

Introduction

A graph in computer science is not the same as the graph you may have encountered, such as y = mx + b. Instead, it is an object represented with a set of nodes or vertices connected by edges.

Graph Theory is the study of graphs! More specifically, it is the study of the properties of graphs, and this article will cover some of the ways we have designed algorithms for computers to analyze graphs.

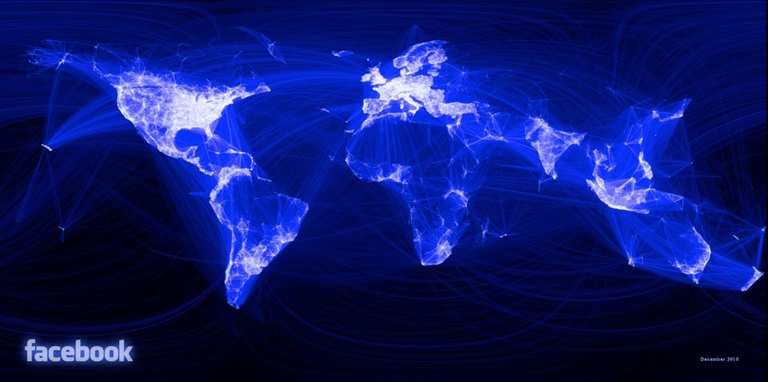
But why do we care? Graphs are able to represent an enormous amount of situations that are extremely important in a variety of fields. In biology, a graph can signify the interactions between proteins in a biological system, where nodes are different proteins and edges represent the interactions. Or perhaps it could model the brain’s structure of neurons and how each cell is connected to each other. In the social sciences, graphs can represent a social network such as Facebook, where edges represent followers or friends!

Once you have a graph, we want to learn some of its properties. For example, if you have a graph of everyone you know, and everyone they know, and so on, you might be interested in finding out the closest path between you and, say, Taylor Swift. That’s where graph algorithms come in.

Graph Theory Basics

But before we dive deep, we have to take a look at the fundamentals of graph theory. Here are a few different types of graphs:

Undirected/directed has to do with the connections represented by the edges. Undirected edges can be thought of as two-way connections (so 1 is connected to 3 and 3 is connected to 1), but in directed graphs, connections are one-way (1 is connected to 3 but not the other way around).

Unweighted/weighted is about the “weight” of the edges. Weighted graphs have numbers associated with each edge that could mean different things in different contexts. It could represent time, cost, distance, or the strength of a connection!

Acyclic/cyclic has to do with cycles - basically, paths in a graph that connect back to themselves. For example, in the graph above, 1-2-3-1 is a cycle with length 3. Cycles are really important in lots of scenarios, where you might need to find a route that ends up back where it started. Acyclic graphs where every node is connected to every other node are called trees, which are really important in different algorithms.

Graph Algorithms

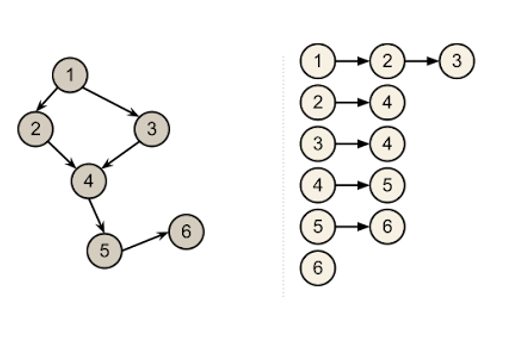
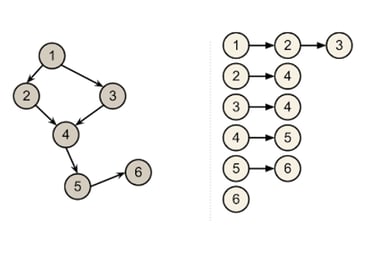
Now, let’s go into some different algorithms regarding graphs! First, we have to figure out how we store graphs in a computer! There are multiple different ways but the one that is most common is called an adjacency list. This is a list of lists where we store all the neighbors of a particular vertex, as seen below.

Depth First Search

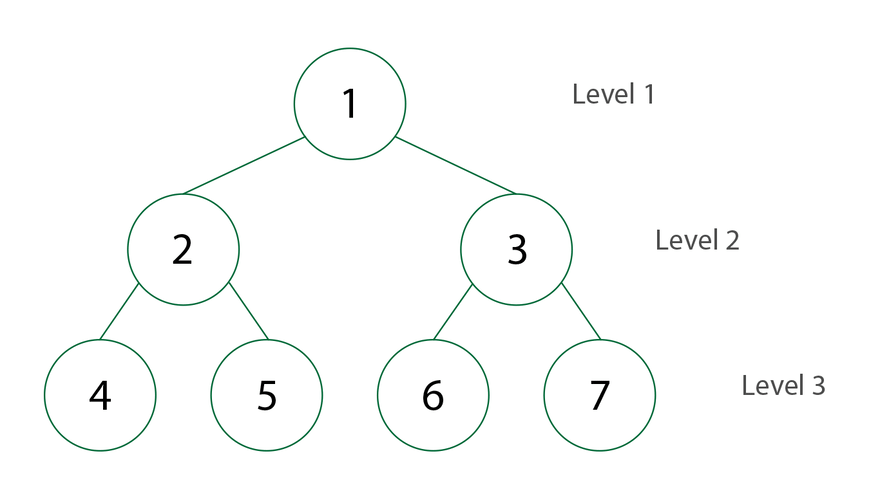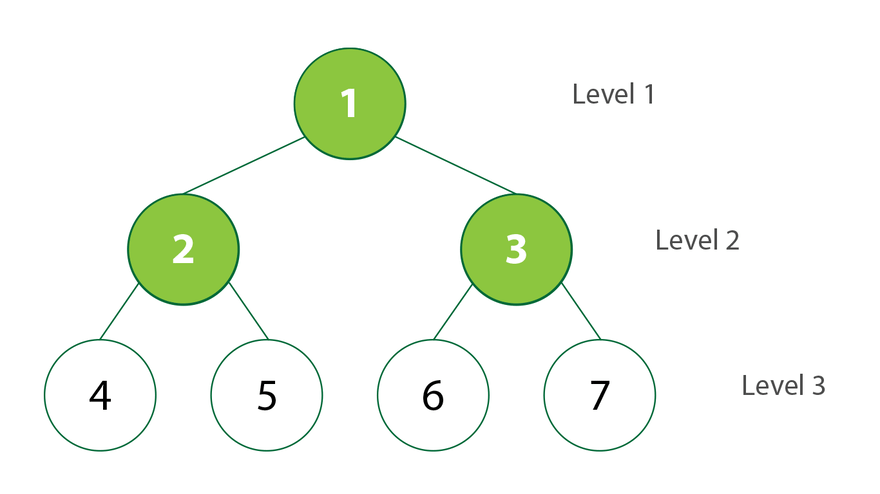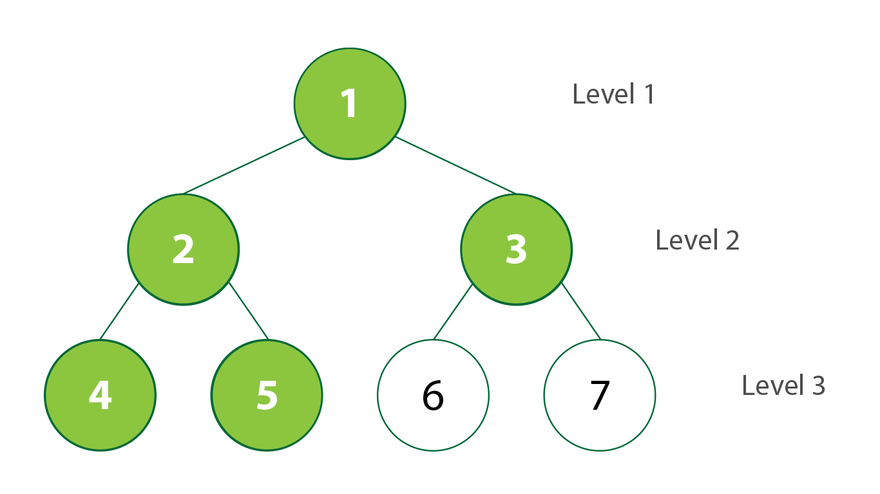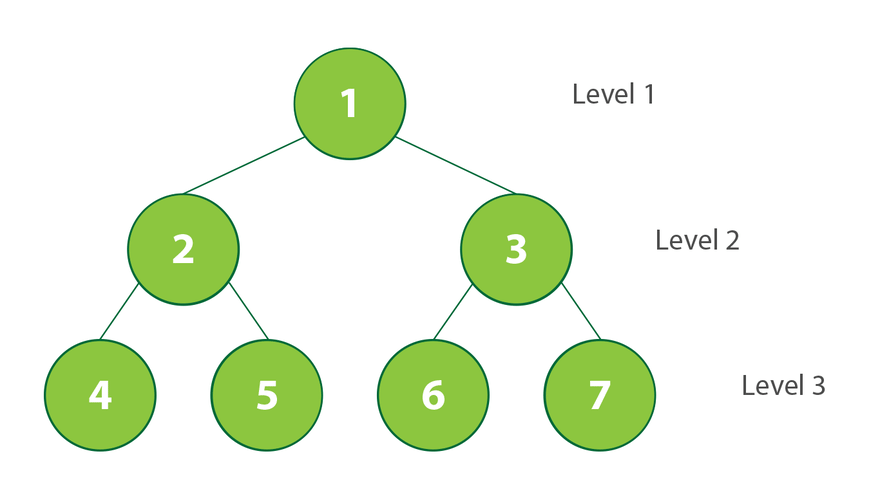
The first algorithm we’ll cover is Depth First Search (DFS). This is essentially a way to traverse a graph, as often we don’t know the size or scale of the whole graph. Think of the Internet as a graph of webpages, where nodes are connected to each other if they contain hyperlinks from one webpage to another. This graph would be massive, but DFS provides a systematic traversal of this graph to visit every webpage! Essentially, you start at a node and keep going between different edges until you’ve hit a node you’ve explored before. Then you backtrack to the node you were just at and visit the next edge from there. Once you’ve hit all dead ends, you’ve explored the graphs! It’s similar to how humans solve mazes - go for as long as you can, then backtrack when you’ve hit a dead end!

Breadth First Search

BFS, on the other hand, explores the graph layer-by-layer. Starting at a node, it visits all nodes at a distance one away, then two away, and so on until it can’t reach any more! It’s sort of like taking a bird's eye view and exploring everything in the vicinity and working your way outwards.

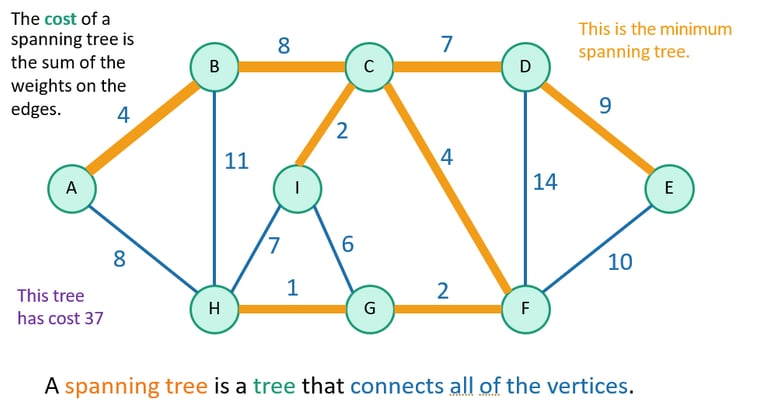
Minimum Spanning Trees

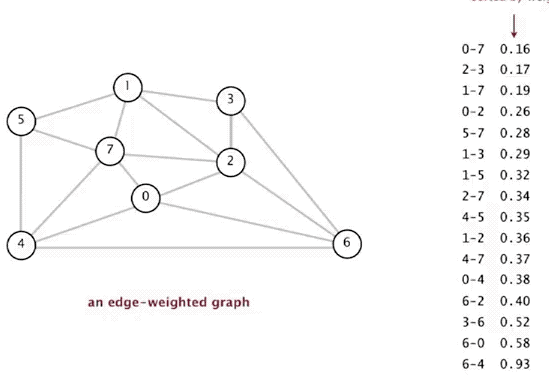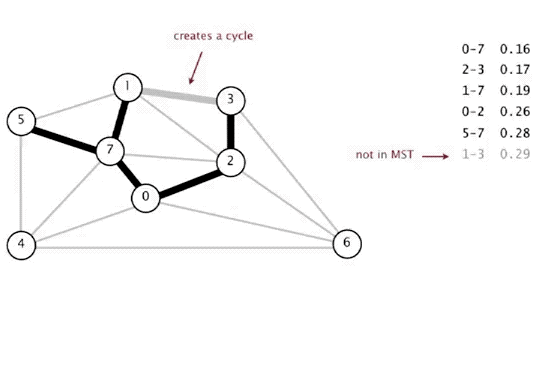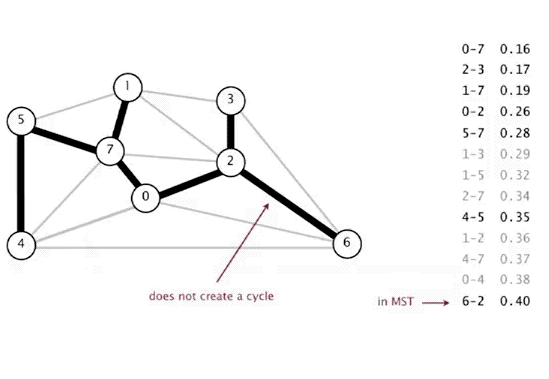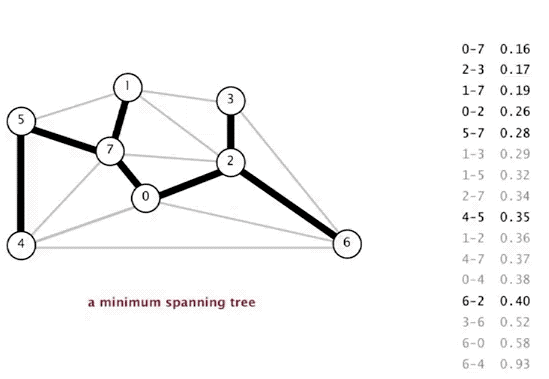
Now let's consider an undirected weighted graph such as the following. Our goal is to find the minimum spanning tree - a tree that connects all of the vertices in the graph with the minimum cost.

This is applicable in many scenarios; if each node represents buildings in a city and the edges between them represent the distances between them - a minimum spanning tree (MST) could represent the tree that would be the most optimal for the placing of telephone wires. It minimizes the total length of wire needed to reach every building in the city - so the whole town gets electricity for the least cost.

However it seems like searching through every possible tree to find the minimum would be extremely difficult - and that is true! There are a lot of possibilities to search through and it would take a computer a long time to run. That's where Kruskal's algorithm comes in! It is an example of a greedy algorithm - where we choose the best option at every step - that doesn't eliminate the final outcome.

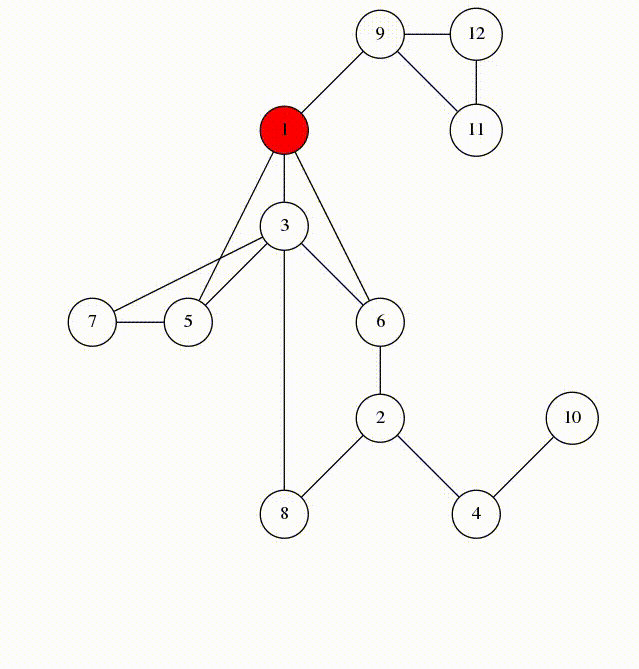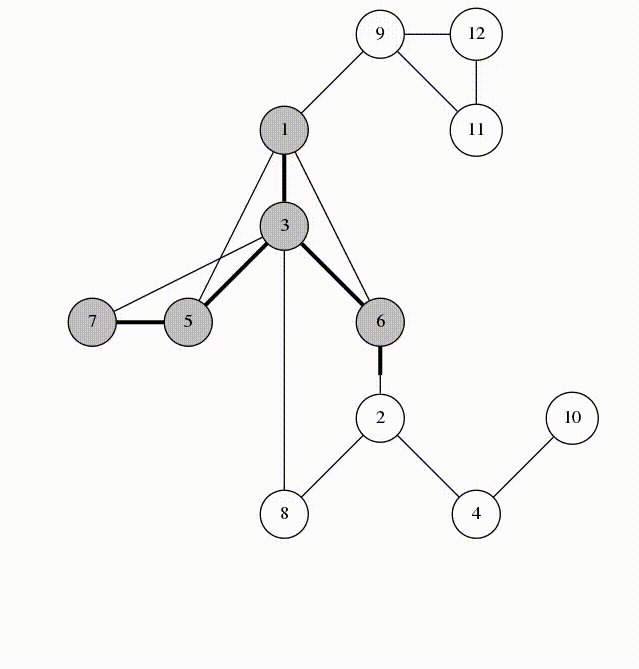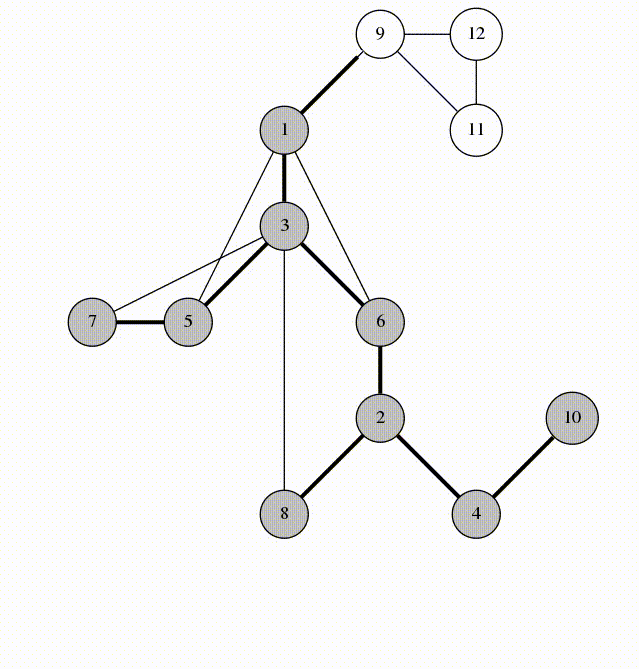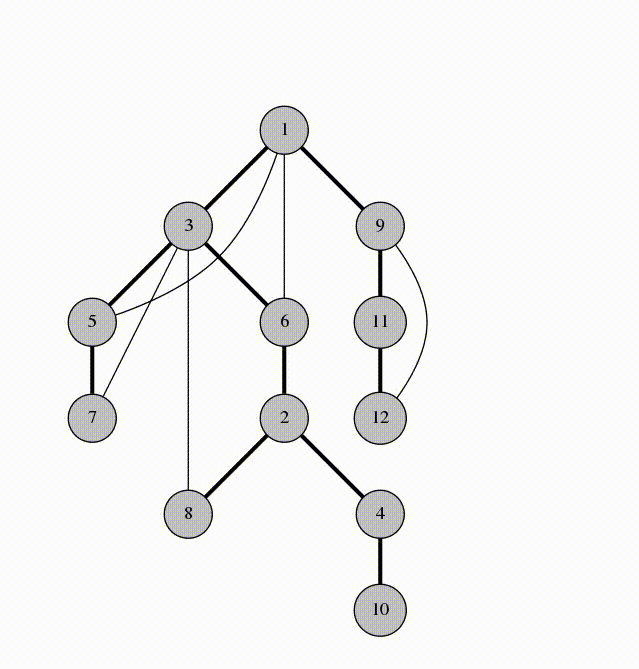
Essentially, we just take the least weighted edge in the graph and add it to our tree! So instead of searching through all trees, we build it from scratch by taking the least edge. However - there is a caveat. If we create a cycle during this process then it wouldn't be a tree. Cycles are actually suboptimal because removing any one of the edges in a cycle still means all the vertices are connected!

So we add a restriction to our algorithm: we take the least edge possible that doesn't form a cycle in our tree!

Shortest Path

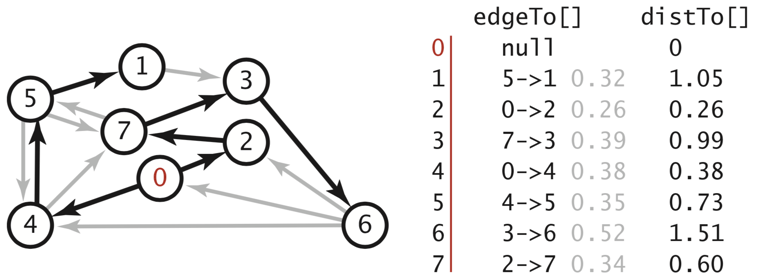
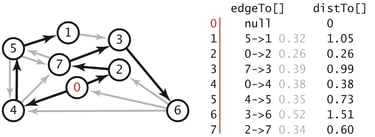
The last algorithm we'll cover is the Dijkstra's algorithm which solves the problem of finding the shortest path from a node to every other node in a weighted graph.

Like Kruskal's, we'll use a greedy algorithm to help us build the shortest path tree which shows the shortest path from a source to all the other nodes.

We essentially keep track of the distances from the source for each vertex, and continually update it throughout the algorithm until it is minimum distance. At each step, instead of choosing the edge with the least weight, we choose the vertex with the least distance and update all of its neighbors with the corresponding distance.

However, there is again another caveat we must consider. If a vertex has already been updated, then it's distance might already be the minimum - so we don't want to update it again. Therefore we only update it, if the new distance is lower!

Conclusion

Graphs underly everything in our modern society - from the Internet, to CPU job scheduling, AI, and so much more. Understanding these algorithms helps you get a deeper understanding of what goes on behind some of the most famous applications - from GPS systems to biological research and everything in between. Hopefully, you can get the intuition behind some of these algorithms and are inspired to learn more.

References

Sedgewick, Robert, and Kevin Wayne. Algorithms. 4th ed., Pearson Education, 2011.